ادامه خلاصه فصل دوازدهم کتاب
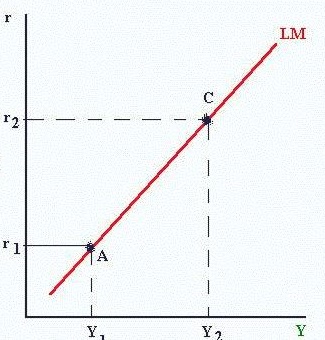
منحنی LM
منحنی LM مکان هندسی ترکیباتی از نرخ بهره (r) و درآمد ملی (y) است که در آن بازار پول در تعادل است. بهعبارت دیگر برای حفظ تعادل بازار پول بین سطح درآمد ملی و نرخ بهره رابطهای مستقیم دارد که اصطلاحا به آن منحنی LM میگویند. (برای فهمیدن بیشتر در مورد نحوه بدست آمدن منحنی LM به کتاب مراجعه نمائید)معادله تابع LM
معادله LM از برابری عرضه و تقاضای پول بصورت زیر بدست می آید:
تعادل بازار کالا و خدمات
تعادل بازار کالا جایی است که عرضه کل و تقاضای کل کالا با هم برابر باشند. در مدل متعارف کینزی فرض میشود که سطح تولید و اشتغال توسط تقاضای کل تعیین میگردد. یعنی محدودیتهای عرضه نادیده گرفته میشود. در یک اقتصاد بسته, تقاضای کل شامل مجموع مصرف, مخارج دولت و سرمایهگذاری میباشد. بمنظور سادگی تحلیل, فرض می شود مخارج مصرفی با درآمد قابل تصرف رابطه مثبت دارد. مخارج دولت بطور برونزا تعیین میگردد, در حالیکه سرمایهگذاری با نرخ بهره رابطه منفی دارد. نرخ بهره نیز متغیری است که در این مدل از تقابل بازار کالا و بازار پول تعیین میشود.
منحنی IS :
منحنی IS مکان هندسی ترکیباتی از نرخ بهره و درآمد ملی است که بیاتگر تعادل در بازار کالا است. منحنی IS نامش را از شرط تعادل بازار کالا گرفته است که در یک اقتصاد بستة بدون بخش دولتی, سرمایهگذاری(I) برابر با پسانداز(S) است. با این فرض که رابطه بین سرمایهگذاری و نرخ بهره منفی است، منحنی IS شیب نزولی دارد.
تابع IS:
بنابراین معادله IS برابر خواهد بود با:
تعادل کل: تعادل همزمان در بازارهای کالا و پول
برای
بحث پیرامون دو بازار پول و بازار کالا و خدمات، دو نمودار هندسی بهدست آوردیم. منحنی
LM مکان هندسی همه ترکیبات نرخ بهره و درآمد ملی تعادلی است، که به
ازاء هر یک از نقاط آن، بازار پول در حال تعادل است. همین طور منحنی IS
یک چنین ترکیبات تعادلی را در بازار کالا، نشان می دهد. حال اگر این دو منحنی در کنار
هم و در یک فضای دوبعدی رسم شود، محل تلاقی آنها، زوج مرتب واحدی از y
و r که هردو بازار را بهطور همزمان در تعادل نگه میدارد،
بهدست آوریم. اگر زوج مرتب نرخ بهره و درآمد در نمودار ترسیمشده در موقعیت y0،
r0 باشد هردو بازار (کالا و پول) در تعادل بوده و هیچ دلیلی
ندارد، که بخواهند از این موقعیّت دور شده و تغییر نمایند.
می توان تعادل همزمان دو بازار را با روابط جبری نشان داد. در صورتی که معادلات IS و LM که در قبل بدست آمده، به صورت زیر باشد، با یک دستگاه دو معادله دومجهولی مواجه هستیم که براحتی می توان آن را حل نموده و مقادیر تعادلی نرخ بهره و درآمد را بدست آوریم:
- ۹۵/۰۳/۱۷
- ۹۸۲۵ نمایش